A couple of weeks ago Ben Bernanke argued in his blog against John Taylor's suggestion that the making of monetary policy should be rule based, and that the rule it should be based on is Taylor's eponymous Taylor Rule.
This rule was based on looking at past interest rate decisions and placing a line of best fit through the response of policy makers to changes in inflation and growth expectations. It was set up to be descriptive of past monetary policy decisions and Taylor believes that it provides a good basis for monetary policy going forwards.
Like any man faced with his job being replaced by a computer, Bernanke responded by voicing the opinion that human discretion would trump robot decision making. Most people tend to agree with Bernanke on this.
It is not that I disagree with Bernanke here, but it brought to mind a study of university admission processes which I now can't find (I have found this one instead which is similar). If you ask any professor who conducts university admission interviews, they will normally state without doubt that their interview adds value to the admissions process. However the study showed that, in the subjects in the sample group, the interview score added no value in terms of predicting the prospective student's final grade. Thus including the interview in the process alongside other hard data such as exam results gave a worse selection of students. The human discretionary input made the selection process worse.
However, when the researchers, instead of taking the actual individual interview scores, did a regression of the qualities that the admissions tutors looked for (using interview scores regressed against qualities shown) - and then they applied a interview score based on the implicit weightings given by the professors - they found that the qualities-weighted interview score proxy was actually a good indicator of performance. So the problem was not that the admission professors did not know what to look for. The problem was inconsistent application of the rules they had in their head but had not formalised.
One could argue, as Taylor does, that the inconsistency of human decision making is sub-optimal and a rule that describes the average decision making gives better results.
How relevant is this idea here? I don't know. For one thing, the researchers had a lot more data than John Taylor had formulating his rule. For another, the experiment assumes that the overall environment is the same in the past as the future (that it is ergodic). It is not clear that the economic situation now can be compared to that when the rule was trained. The third criticism would be that when a descriptive rule becomes prescriptive it can change the reaction of the system that it is supposed to describe.
Overall, I am probably more on Bernanke's side here. But actually that whole discussion was something of a digression. The main point here is to talk about the real danger of using the Taylor rule - a danger that is orders of magnitude larger than that described by Bernanke.
To do so, I need to go back to my flows model of the economy first discussed here. It takes nominal GDP at the end of one time period and looks at money spent during the next time period to give nominal GDP at the end of the next time period. It is very simple and, because it is set up as an accounting identity, unless I have made an error in setting it up, it should be correct.
The flows model connects GDP at time t to GDP at time t+1 like this:
At the beginning of every time period all the money is paid out and then during the time period it is either spent or saved. At the beginning of next time period we start again.The sources of money are:1) 'GDP' from work done the previous time period.2) 'New Cash' printed by the Central Bank, C. This could, in theory, be negative.3) 'New Loans' created by private banks, L. This could also be written as New Deposits. This can be positive or negative.4) Money taken 'From Existing Savings' to be spent in the economy. Eg pensioners spending their private pension. In terms of the Stocks model, the existing savings, ES, can be seen as the sum of CB cash, equity and debt.The GDP is divided into three flows:a) Dividends - this includes eg. rental payments on houses. It is any return on equity as defined in my post on Stocks. This is denoted by d.b) Interest, i.c) Wages, w.There is not much more required for this simple system in order to calculate the path of nominal GDP. Real GDP depends on actual productivity increases, but nominal GDP in this closed system is just how much money is spent (if there is more money spent but no increase in productivity then it is just inflation). To calculate the nominal GDP and net new savings/debt, I just need to put in how much is spent on consumption.
I will call α the coefficient of consumption. So αd is the proportion of the dividends paid that are spent in the economy. Similarly, αi, αw, αL and αC are the coefficients of consumption of interest, wages, new loans and new cash. Also, I will define γ as the proportion of existing savings that are spent in the year.
We can then find the next year's nominal GDP and the amount of net savings by using the following:
GDP(t+1) = αd*d + αi*i + αw*w + αL*L + αC*C + γ*ES (1)
And we can define Unspent Income (UI) as:
UI = (1-αd)*d + (1-αi)*i + (1-αw)*w + (1-αL)*L + (1-αC)*C - γ*ES (2)
In order to proceed further, I will need to provide a new concept of equilibrium. This is not a Neo-Classical equilibrium; it is the equilibrium of an economy that does not need further debt to achieve GDP potential. For this equilibrium, the following must apply:
Equilibrium:
γ*ES = (1-αd)*d + (1-αi)*i + (1-αw)*w + (1-αC)*C (3)
This means that the spending of existing savings exactly matches the amount being saved without any new debt being taken out.
This is the true equilibrium in an economy that we need to aim for.
In any case, you can see how the dividends, interest and wages from GDP at time t, as well as the external sources of money (from existing savings, new loans and new central bank money) make up the next period nominal GDP.
What has gone wrong:
I would say that during the 1945 to 1975 period, a period of excellent growth across the developed world, we were broadly in equilibrium (or at least the total private debt levels were low enough that it didn't matter). The savings broadly matched the spending of exisiting savings. Governments, using Keynesian policy tools would increase their spending (the government component of L) when savings were too high and reduce when more savings were being spent than new savings made. It all worked pretty well.
What changed in the 1970s was the rise of credit. Looking at the Equilibrium equation (3) above, the share of GDP going to interest and dividends went up relative to the share going to wages. The coefficients of consumption (α) for the interest and dividends is lower than that for wages so we had the following inequality:
γ*ES < (1-αd)*d + (1-αi)*i + (1-αw)*w + (1-αC)*C
This means that the economy is out of equilibrium. The GDP shown in figure 1, will now go down because of the excess savings.
Previously fiscal policy would have been used to stimulate growth and return the system to equilibrium.
Increased government debt is far more efficient at stimulating the economy than increased private sector debt. I show here that a 10% net increase in private sector debt stimulates the economy and adds approximately 1.1% to GDP growth in the year that the debt is taken out. So the multiplier of private sector debt to GDP here is 11%. However, the cost in future years due to the increase of interest repayments at the expense of wages is 0.15% of GDP for every year going forwards.
The same amount of increased government debt costs only 0.9% of GDP going forwards, but crucially the multiplier on this spending is much higher. Therefore much less government debt is needed to create the same amount of economic stimulus as private sector debt. In fact, I estimate that government debt is an order of magnitude more efficient.
But from the early 1980s, policy makers deregulated markets and switched to monetary policy as the tool of demand moderation. They used something equivalent to a Taylor rule before the Taylor rule was invented.
How does the Taylor Rule work - using the Flows model:
As Wikipedia will explain it better than me, I will give their definition of the Taylor Rule:
According to Taylor's original version of the rule, the nominal interest rate should respond to divergences of actual inflation rates from target inflation rates and of actual Gross Domestic Product (GDP) from potential GDP:
is the target short-term nominal interest rate (e.g. the federal funds rate in the US, the Bank of England base rate in the UK),
is the rate of inflation as measured by the GDP deflator,
is the desired rate of inflation,
is the assumed equilibrium real interest rate,
is the logarithm of real GDP, and
is the logarithm of potential output, as determined by a linear trend.
In this equation, bothand
should be positive (as a rough rule of thumb, Taylor's 1993 paper proposed setting
).[7] That is, the rule "recommends" a relatively high interest rate (a "tight" monetary policy) when inflation is above its target or when output is above its full-employment level, in order to reduce inflationary pressure. It recommends a relatively low interest rate ("easy" monetary policy) in the opposite situation, to stimulate output. Sometimes monetary policy goals may conflict, as in the case of stagflation, when inflation is above its target while output is below full employment. In such a situation, a Taylor rule specifies the relative weights given to reducing inflation versus increasing output.
So the Taylor rule states that the nominal short term interest rate should be a function of the difference between current inflation and desired inflation and the difference between the current rate of GDP growth and the potential GDP growth - which is GDP when the economy is at full capacity (to get this he suggests linear trend extrapolation). Using Taylor's rule of thumb above, it suggests that a 1% increase in inflation should correspond to a 1.5% increase in interest rates and a 1% decrease in growth should correspond to a 0.5% increase.
How does this work in our Flows model? Looking at the equation for GDP (1) we can see that if the right hand side of the equation gives a GDP lower than potential, the monetary policy needs to adjust the right hand side to increase the total.
How would lowering interest rates increase the total GDP. There are three ways:
1) It would increase the appetite for new borrowing - making L go up.
2) It would increase the value of assets - making ES go up.
3) It would increase the spending of existing savings - making γ go up.
I would say that the biggest impact here is 1); it increases the amount of debt in the economy.
But by increasing the amount of debt what does it do? It pushes the system further away from equilibrium in equation (3). Interests payments in the next period go up, and so demand is further reduced. And GDP goes further from potential in the next time period. So interest rates need to be reduced further next time. This continues until we reach the lower bound. Here is a graph of the US 10 year government bond rate since 1975 - the trend is clear apart from the spike in the early 1980s, and we now have the lowest interest rates ever:
One more minor point which I disagree on, is that the inflation targeting does not separate inflation with a domestic source compared to that with a foreign source. I discuss the error that I believe that they are making here.
But the main problem is that, as with the whole orthodox macroeconomic profession it seems, is that IT IGNORES PRIVATE SECTOR DEBT.
I can not stress how obviously important this is. It assumes that debt can grow indefinitely. It assumes that previous debt has no impact on growth. It ignores financial instability. And ultimately, it creates a positively reinforcing feedback mechanism that ends in the zero lower bound and economic stagnation.
This is the real danger of the Taylor rule, Dr Bernanke.
And the solution, once again I point out, is to regulate the money supply not using interest rates but by using central bank cash. I describe here why it is an economic crime for an economy to be running under capacity because of lack of money. And I describe here why printing money for government expenditure is essentially the same as the government borrowing to spend in a Keynesian framework, just at 0% interest rate indefinitely. There is nothing to fear from allowing the government to create money instead of relying purely on private sector debt to fuel the economy. The sooner we realise this, the better for us all.
This is not even ideological. The money could be spent on research, infrastructure, education and other investment; in my opinion this is the most sensible place to start. But it could be given in tax cuts to lower income workers. Or it could be given as tax cuts to top rate tax payers - although more money would be needed to keep the spending at the same level due to the higher rate taxpayers' lower propensity to consume. The important part is to work out a multiplier on the spending and make sure that total spending of money created matches the amount taken out of the economy by savings.
This is not even ideological. The money could be spent on research, infrastructure, education and other investment; in my opinion this is the most sensible place to start. But it could be given in tax cuts to lower income workers. Or it could be given as tax cuts to top rate tax payers - although more money would be needed to keep the spending at the same level due to the higher rate taxpayers' lower propensity to consume. The important part is to work out a multiplier on the spending and make sure that total spending of money created matches the amount taken out of the economy by savings.
It is my view that, due to the debt levels and corporate rent seeking, we have a structural and chronic problem of excess savings in the economy. We have only three choices to keep demand up. 1) Private Sector Debt, 2) Government Debt and 3) New Government money. By refusing to use choice (3), we are forcing upon ourselves (1) and (2). And the eventual consequences will not, I fear, be pleasant.
Unfortunately I worry that it will take a long stagnation before we work it out.
Unfortunately I worry that it will take a long stagnation before we work it out.
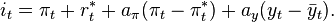


"Eg pensioners spending their private pension."
ReplyDeletePrivate pensions are rarely in cash. They are in instruments which have to be sold to somebody else (i.e. no net effect).
Running down of 'rainy day funds' yes. Pensions, no. Pensions are asset transfers between current economic participants.
The instrument is sold for cash to another saver. Then the cash is spent. One could argue over the gap between the propensities to spend of the two participants but I think probably the pensioner's is higher.
DeleteAnyway, whichever is correct, I think you got my general point there!